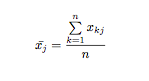エコノミスト誌（6/4号；使える統計学）を考察するための統計学的な量について
今回は、先のログの続きとして、エコノミスト誌の記事（6/4号；使える統計学）を統計学的に表現する前準備として、基本的な統計量を示しておく。
変量と観測データは、先のログと同じに以下の表のように表現されるとする。
ここで、列は変量を表し、行はサンプルを表している。
標本平均（算術平均）
第j番目の変量Xj の観測値の標本平均とは、以下の式で計算される量のことをいう。
変量Yの観測値の標本平均とは、以下の式で計算される量のことをいう。
平方和と分散、標準偏差
変量Xi の観測値の平方和とは、以下の式で計算される量のことをいう。
また、平方和をサンプルサイズで割った量を分散、その平方根を標準偏差という。
上に対して、以下の式で計算される量を、母分散の不偏推定量であることから不偏分散とよぶ。
変量Y の観測値の平方和とは、以下の式から算出される数量である。Yに関しても、Xiと同様に分散、標準偏差、不偏分散が定義される。
積和と共分散
変量Xi とXjの観測値の積和とは、以下の式で計算される量のことをいう。
また、これをサンプルサイズで割ったものを共分散という。
変量Xi とYの観測値の積和とは、以下の式で計算される量のことをいう。
例
Y=X+10という式をベースにして、明らかに相関があるXとYの散布図を作成してみた。
データは100組の（X、Y）をRによって算出した。以下にプログラムを掲載しておく。
> #乱数より相関のあるデータを作成する。
> vx <- c()
> vy <- c()
> for(i in c(1:100)){
+ x <- runif(1)*10
+ y <- x + 10 + rnorm(1,mean=0, sd=1)
+ vx <- append(vx,x)
+ vy <- append(vy,y)
+ }
> #散布図
> plot(vx,vy)以下に、平均値など上に記した統計量を算出するコードを掲載する。
相関係数はcor()によってベクトルから１回で計算できるが、XとYの平方和、積和から算出した結果も会わせて掲載しておく。
> #平均値
> mean(vx)
[1] 5.409325
> mean(vy)
[1] 15.44853
> #組み込み関数で相関係数を求める
> cor(vx,vy,method="pearson")
[1] 0.9481843
> #平方和と積和から相関係数を求める
> sxx <- t(vx-mean(vx))%*%(vx-mean(vx))
> syy <- t(vy-mean(vy))%*%(vy-mean(vy))
> sxy <- t(vx-mean(vx))%*%(vy-mean(vy))
> sxy/sqrt(sxx*syy)
[,1]
[1,] 0.9481843
